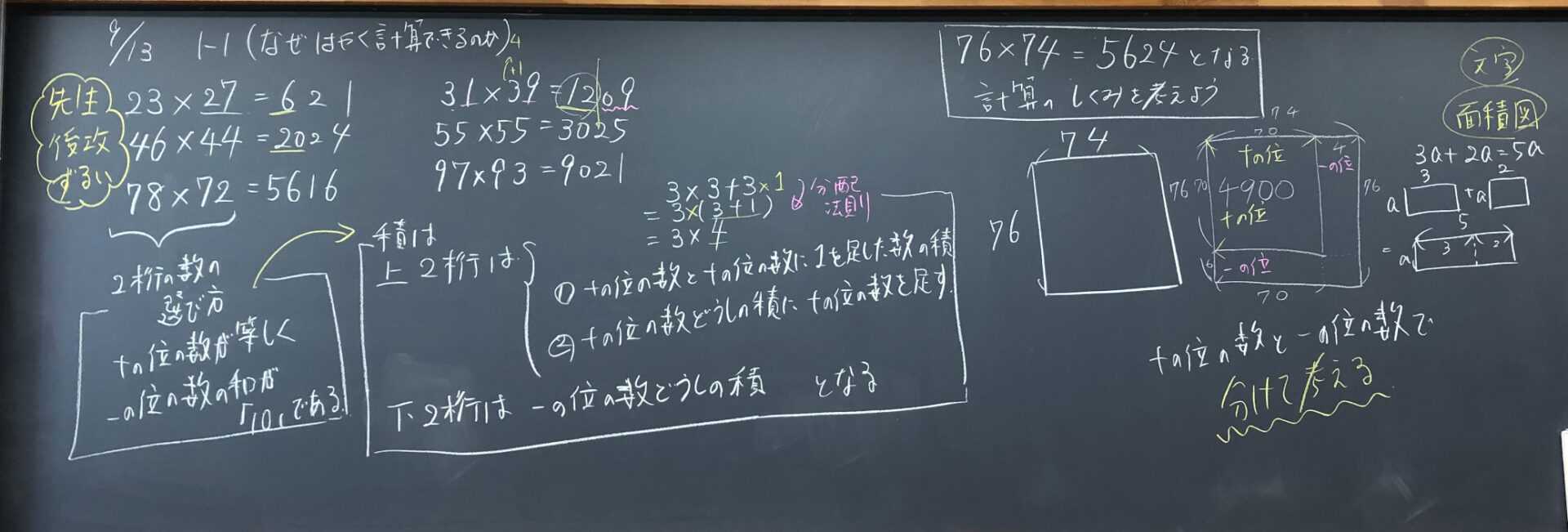夜中暑くて冷房の温度を1度下げたら、今度は寒くて布団に包まる数学教師
#1度でこんなに違うもの?
#自分にとっての適温を知りたい
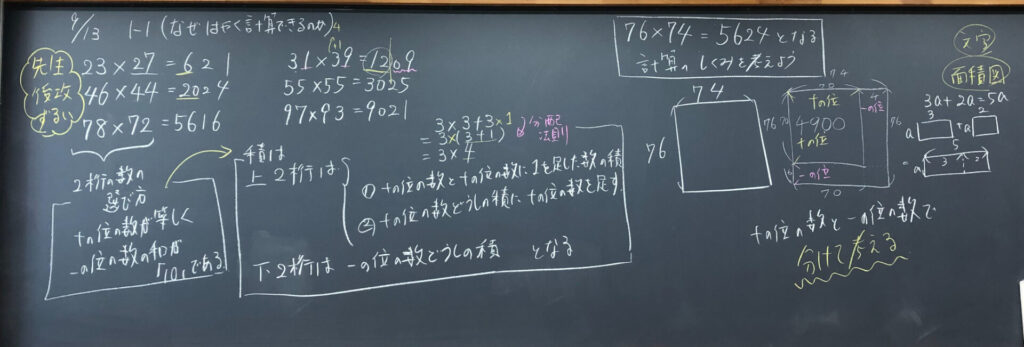
1⃣ 問題
ある2桁同士の掛け算で、早く計算できる仕組みを考えよう。
2⃣ 活動の流れ
本時は、担当する中学三年生との最初の授業でした。学習評価や持ち物、授業に対する心構えなどについて、プリントを使って説明した後に、おこなった授業となりました。
初めての授業ということで、多くの生徒が安心して取り組めることや関心を高められるような展開に努めようとしました。
初めに先生は2桁の掛け算がとても早いと紹介して、実際に生徒と勝負する場を設けました。
生徒に好きな2桁の数字を言ってもらい、先生はそれに対する2桁の数字を言い、求められた積を答えます。
もちろん、タネも仕掛けもありますので、先に生徒が2桁の数字を言ってもらわないと先生は勝負に勝てません。1人目の勝負で、「生徒に先に数字を言わせるのは何か仕掛けやあるのではないのか」と怪訝そうにしている生徒もいると思います。そのような生徒に後で考えを発信してもらうように覚えておきます。
2人目の勝負でも、先に数字を言ってもらいますが、生徒側から「ずるい」とか「先生が先に言ってほしい」などと発言があるかもしれません。そのような声にいいとろに気づけていることを伝え、価値づけします。もちろん、生徒に先に数字を言ってもらい、それに対応する数字を先生が言い、すぐに積を答えます。
全体がザワザワと周りと話したそうだったり、確認したそうな雰囲気を感じたら、一度、自由に相談させます。何か気づいたことがある人と挙手をさせて、発言はさせずに、3人目の勝負をおこなってもよいと思います。
私は、相談せてから、3人目の勝負の場を設けました。
3人目の勝負では、生徒の2桁の数字を言ってもらった後、「先生が言う2桁の数字が分かる人?」と問いました。半分くらいの生徒は気づき始めていました。メモをしている生徒も何人かいました。
実際に、先生の数字も言い、2桁同士の積がすぐに分かる人を挙手させて、何人かに当てました。
その積が合っていることを伝え、もう一度、近くの人と話合う時間(3分くらい)を設けました。
話し合い後、2つの2桁の数字の選び方についてまとめました。
積については、例を増やし、生徒の言葉を受け止めながら、数学的な用語でまとめていきました。
76×74=5624の計算のしくみを考えてもらいました。
計算のしくみを考えるうえで、どのような方法を取ればよいのか、全体に問いました。
同一学年でやらせてもらい、3年目ということあり、「面積図」で考えることがよいと発言がありました。
もし、そのような学年でなかった場合は、3a+2a=5a の計算のしくみを考えるときに、面積図を用いたことを確認したと思います。
76×74=5624の計算のしくみを面積図を用いて、考える時間を設けました。一人でも考えても、近くの人などと話し合ってもよい時間にしました。
十の位と一の位を分けて考えていることをポイントとなるため、そのような考えをしている生徒に価値づけをして、時間となりました。
次のブログに次時は書こうと思います。
読んでくださった方の人生がいつまで輝き続けますに。