家に学校用の黒板を設置したい数学教師
#板書が大好きすぎて家でも書きたい
#絶対要らない
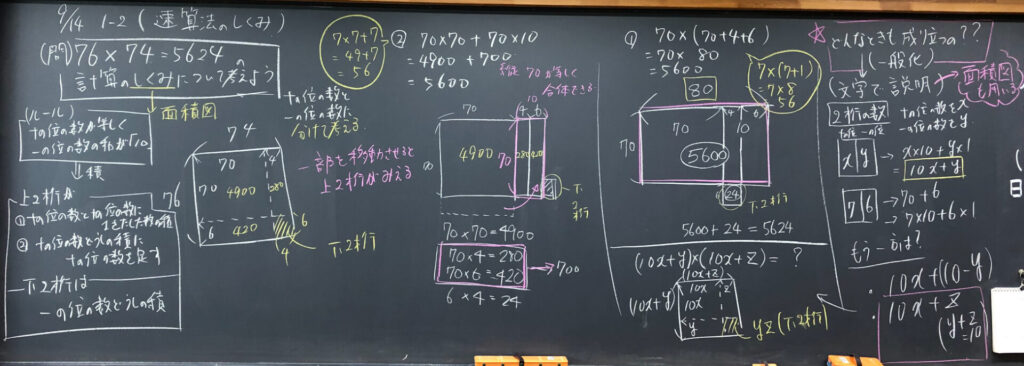
1⃣ 問題
76×74=5624 の計算のしくみについて考えよう。
2⃣ 活動の流れ
前時からの続きを学習となるので、仮定と結論を確認することから入る。
仮定(ルール)
2桁の数同士の乗法において、十の位が等しく、一の位の数の和が10となるときに速算で積が求められる。
結論(積)
上2桁について、
①十の位の数と十の位の数に1を足した数の積
②十の位の数同士の積に十の位の数を足す
下2桁について、
一の位の数の同士の積
計算のしくみを考えるときに「面積図」が有効であることを確認して、各自思考(近くの生徒と相談OK)の時間を設ける(10分くらい)。
机間指導の中で、面積図①の図形を十の位と一の位を分けて、面積図②や③のような考えを持っているを見つけたい。

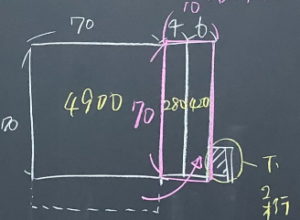
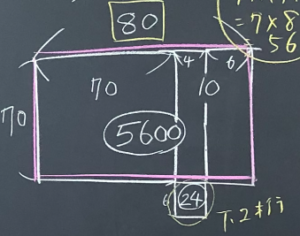
面積図②や③のように考えている生徒をみつけ、各自思考7分くらいから概要となる図を板書させる。完全に説明した図を書かない(図形の一部を移動ことだけをかかせるなど)で、分かっていない生徒に対してヒントになることを期待する。
また、式と図のリンクさせることも大切にしたいと思っているが、
結論の
上2桁について、
①十の位の数と十の位の数に1を足した数の積
7×8=56
上2桁(百の位と千の位に直すと)
→70×80=5600
②十の位の数同士の積に十の位の数を足す
7×7+7=56
上2桁(百の位と千の位に直すと)
→70×70+70×10=5600
①と②の見方の違いが、式の形にも違いが出てくることに配慮したい。
解決の糸口となる、『面積図を移動させること』が、今後の「式の展開や因数分解」にもつながるため、しっかりと価値づけをしていきたい。
そして、式と図のリンクについては、①と②の違いも含めて、丁寧に全体で説明してく必要がある。
特に、76と74の一の位の(6+4)=10となることで速算ができることを面積図で確認しながら理解を深めさせたい。
最後に、具体的な76×74で考えたが、『どんなときでも成り立つこと』を説明するには文字を使う必要性を確認する。
(多項式)×(多項式)を学習していくので、(10x+y)×(10x+z)の計算はできないかもしれないが、既習である(多項式)×(単項式)や面積図の見方から、統合的・発展的に考察することの意味にふれられる機会にしたい。
読んでくださった方の人生がいつまで輝き続けますに。