スカシッペをしたときに、妻に必ずバレる数学教師
#すかし切れない表情
#実は臭いでバレてる説
1⃣ 問題
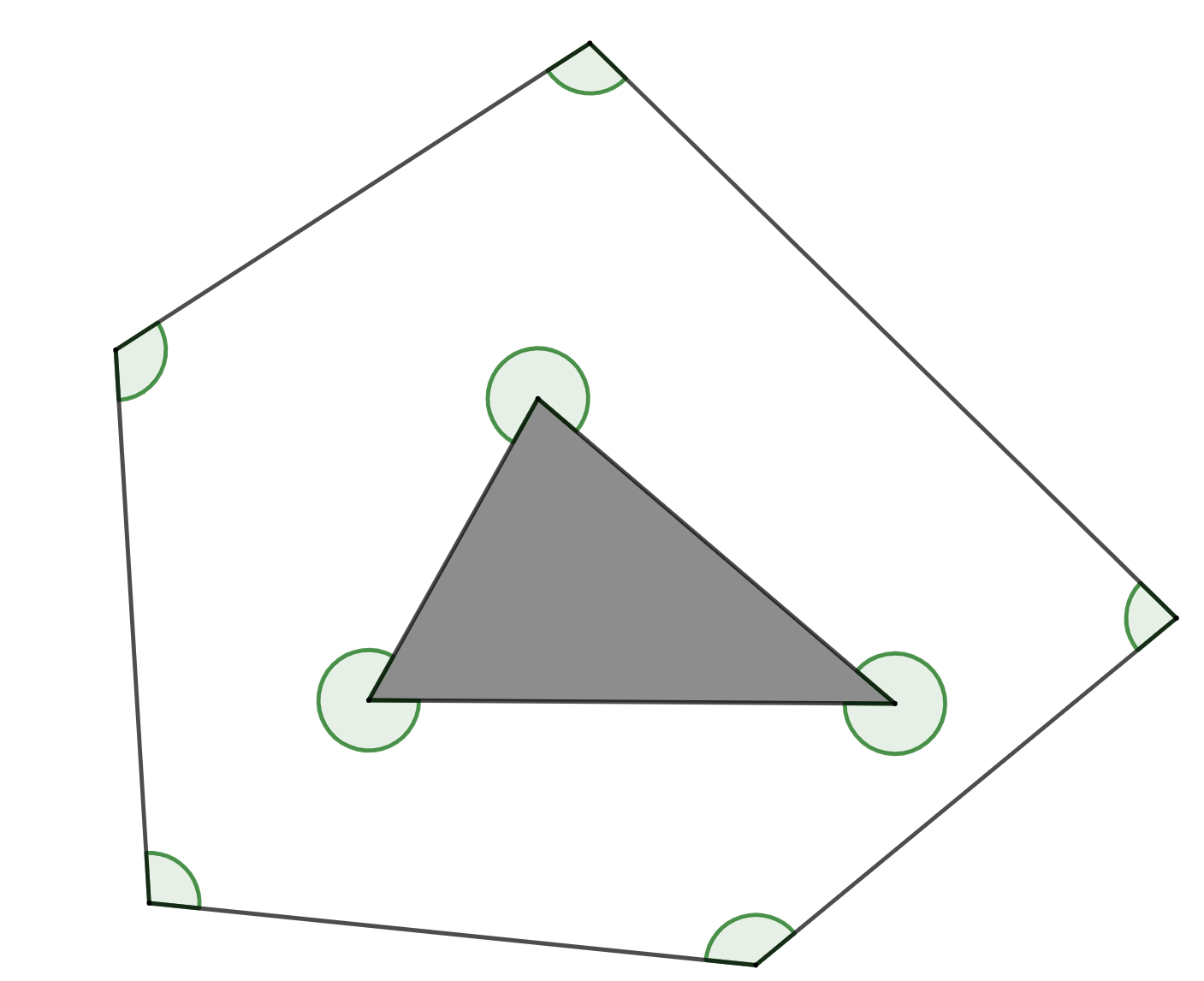
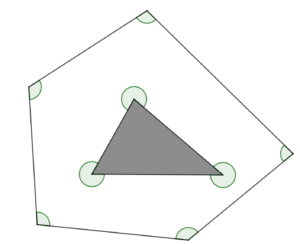
穴あき図形の内側の角度の和をいろいろな方法で求めよう。下図のような図形を「五・三角形」と呼ぶことにします。
2⃣ 活動の流れ
まずは予想させたい。直感でよいので、生徒の意見を取り入れ、主体的に考えるきっかけをつくりたい。また、見当がつきにくいが、90°の倍数などに偏ったりすることも予想される。直感といっても、当てずっぽうな数値でないことも生徒をほめる良いチャンスになるだろう。
各自で考える時間をつくる(5分程度)。
巡回中に、最低2つの考え方が出るようにしたい。
①三角形や四角形に分けて求めている方法
②外角の和が360°であることを活用している方法
その後、グループで話し合い、求める方法を掲示用のプリントに書く。
その時に教師は、色々な方法が黒板に提示できるように巡回しながら、アドバイスをして回る。
大体、3~4くらいの方法になると考える。前で生徒に各方法の説明をしてもらい、教師はまとめをする。
その後、他の穴あき図形について考えさせたい。教師側ではなく生徒からの意見で課題とすることが望ましいと考える。2つの方法を提案したい。
①各自思考やグループでの話し合いの中で、他の図形を考えている生徒を見出す。
→この流れで、課題を全体共有するには、普段の授業から「条件を変えて考える」ことをする必要がある。各授業で余力のある生徒(早く解決した生徒)が自ら「条件を変えて考える」場面があったときに、全体で共有する。模範となる行動に脚光を当てることで、その生徒は次もおこうだろう。また、他の生徒も見本となる行動を示されたため、真似ることをするだろう。
②教師の発言から生徒の考えを引き出す。
→「他の穴あき図形も求められそうですか?」「どんな穴あき図形でもできそうですか?」「(普段、一般性と求めることが多いことを前提で)じゃあ、今日の授業はこれだけにしようか(喜ぶ生徒もいれば、他にも考えたいと思う生徒もいると思われる)」
最終的には、どんな穴あき図形でも内側の角の和を求められることを目指す。穴あき図形の一般性に気づかせたい。
今回は色々な穴あき図形を求め、一般性にせまる方法を選んだ。
自分が求められそうな穴あき図形を選び、全体で共有する。
共有することで、一般性に気づかせたい。
全体で共有する前に、一般性に気づく生徒も出てくる。そのような生徒には、なぜそのようなのか根拠も考えさせたい。
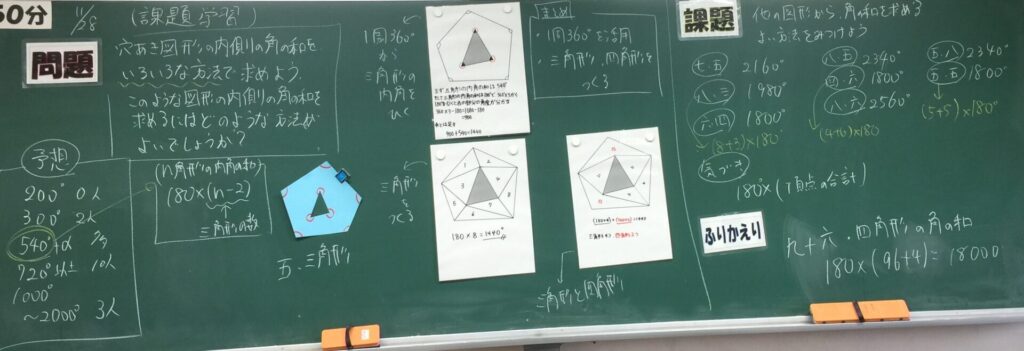
この授業では、前半は多角形の内角の和、外角の和についてまとめる。
後半は、一般性に気づくためには、ある程度のデータを集めることが大切だということを感じてほしい。
読んでくださった方の人生がいつまで輝き続けますに。