① 問題1提示・解決(10分)
(問題1)
点Aから3cmにある点をかこう。
問題提示をしてから、各自思考の時間(3分)をとり、机間指導をします。
(机間指導でおこないたいこと)理解度順
△:分からない、1点のみしか書けていない→点Aから3㎝の点をかくように促す。
また、「その1点以外にもないだろうか」と考えを促す。
◇:複数の点が書けている。
○:点の集合が円になることを理解している。
教師が点Aから3cmの点を複数かく。その時に、円になることが見えてくるように、まんべんなく点をとるとよい。
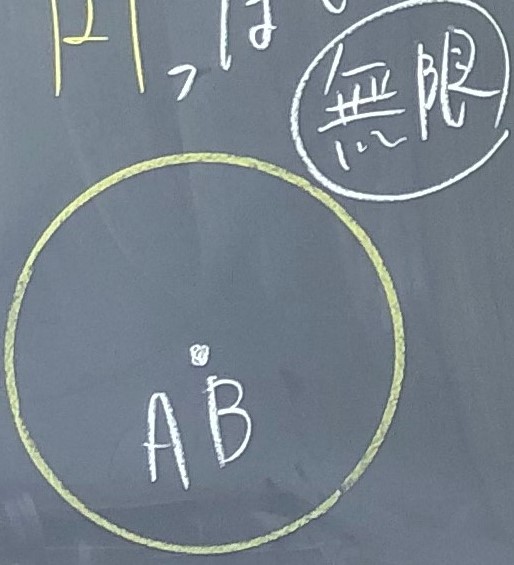
S1「先生、もう(それ以上)点をかかなくてもいいです。無限にあって、円になると思います。」
T「とてもいい見方ですね。S1さんが言ったことが分かりましたか。周りの人と話し合ってみましょう。」
生徒同士の説明や話し合いで、理解が深まったところを見計らって、点の集合が円になるとまとめます。
② 問題2提示・解決(15分)
(問題2)
点Aと点Bから3㎝にある点をかこう。
問題1同様、問題提示をしてから、各自思考の時間(3分)をとり、机間指導をします。
(机間指導でおこないたいこと)理解度順
△:分からない→点Aと点Bをかかせ(なるべく近い方がよい)、点Bから3㎝にある点
(の集合)をかく。書けない場合は問1を参考にさせる。点Aも同様にかかせる。
◇:1つの場合において、問題の条件を満たす作図ができている。
「この場合だけでよいのか。」「これ以外に考えられる作図はないだろうか。」
「点Aと点Bが他の位置の場合はどうなるだろうか」
○:3つ以上の場合について考えることができる。
◎:上記を満たし、「3cm」の条件を変えたときにどうなるのか、考えている。
「3㎝にある点」から一般性を考えようとしている。
4つの場合が考えられます。生徒に板書してもらってもよいでしょうし、なるべく正確な図の感覚を養うために教師が板書してもよいと思います(生徒に説明してもらいます)。
また、板書する順番は、
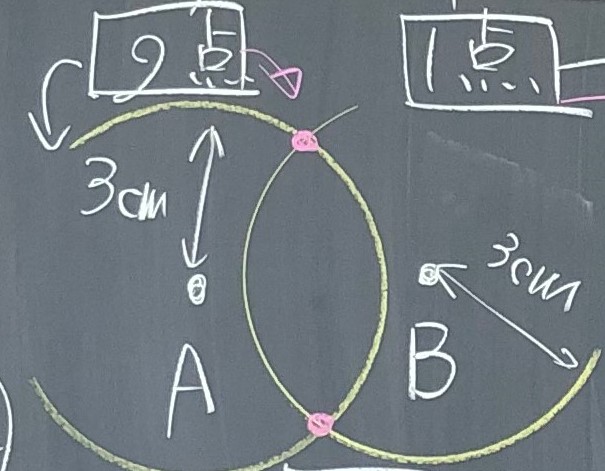
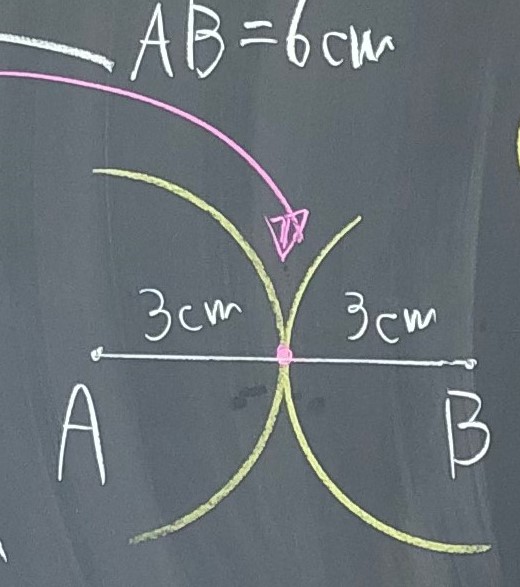
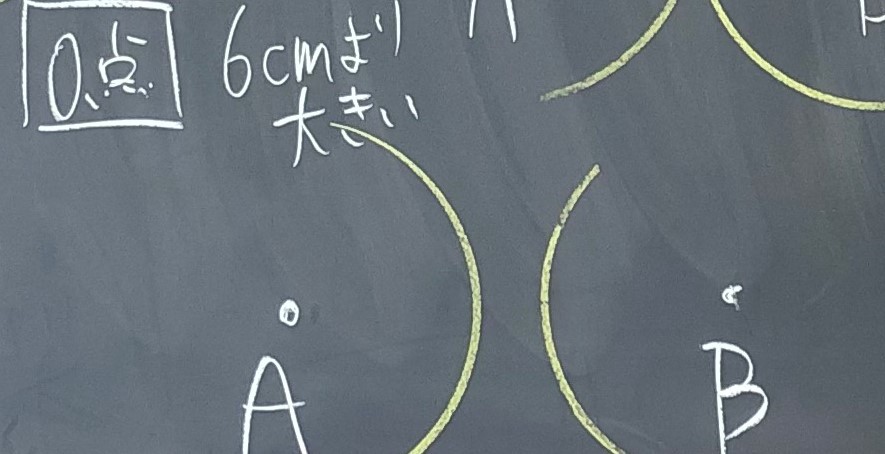
①2点で交わる場合
②1点で交わる
③0点で交わる
④点Aと点Bが重なり、交わる点が無限にある
にしました。
生徒の反応が多いのは、①か③だと思います。ただし、③は生徒が誤答と誤解して消してしまう生徒もいるでしょう(机間指導で気づいたら、大切な考えは消さないように助言する)。よって、①が最初に板書すると、安心した反応になると思います。その後、②としたのは、点Aと点Bが少しづつ、離れていくような感覚も持ってもらうためです。
④を最後にしたのは、気づいた生徒が少ないためです。点Aと点Bは違う位置としている生徒がほとんどだと思います。ただし、動的な視点を持たせつために、紹介します。点Aと点Bを話していく感覚を養い①→②→③、最後に点Aと点Bを近づけて、重なるイメージを頭の中で処理してほしいと思っています。
本時では、試みなかったのですが、イメージしてからgeogebraなどの作図ツールでみせても良かったと思いました。
③ 問題3提示・解決(15分)
(問題3)
点Aと点Bから等しい距離にある点をかこう。
問題3の提示の前に、問題1から2へ問題の条件の変化を確認します。
問題3の提示のときに、問題文を生徒に少し考えてもらいました。自ら条件を変えて問題を作り、一般性を見出す方法を身に付けてもらうためです。
→

(机間指導でおこないたいこと)理解度順
△:分からない→適当に点Aと点Bをかき、(教師が点Aと点Bの距離が目分量で測り、
2点で交わるような)□□㎝にある場合を考えてもらう。
それが終わったら、▽▽㎝の場合も考えてみようと促す。
◇:複数の点が書けている→他の点もかけそうかを聞き、
もっとかいたら点の集合はどうなるだろうかと発問する。
○:点の集合が直線になることが分かる→なぜ直線になるのかを考えさせる。
問題3の解決は全体で確認しました。複数の場合を板書し、他の点も無数にかいたら、点の集合はどうなるかを考えてもらった。
T「他にも点Aと点Bから等しい距離の点をかけそうですか。その点の集合はどのようになっているだろうか。」
S2「直線(っぽく)になると思います。」
T「みなさんも同じですか。」
(生徒は同意しているような表情)
T「では、なぜ直線になるのでしょうか。周りで話し合ってみましょう。」
机間指導の中で、ひし形に着目している生徒がいたら、(適当なタイミングで)全体で共有したいです。本時では、説明できそうな生徒は見つけられませんでした。でも、ある距離の点から等しい2点を結んでひし形を作っている生徒はいたので、その補助線がヒントになることを伝えました。
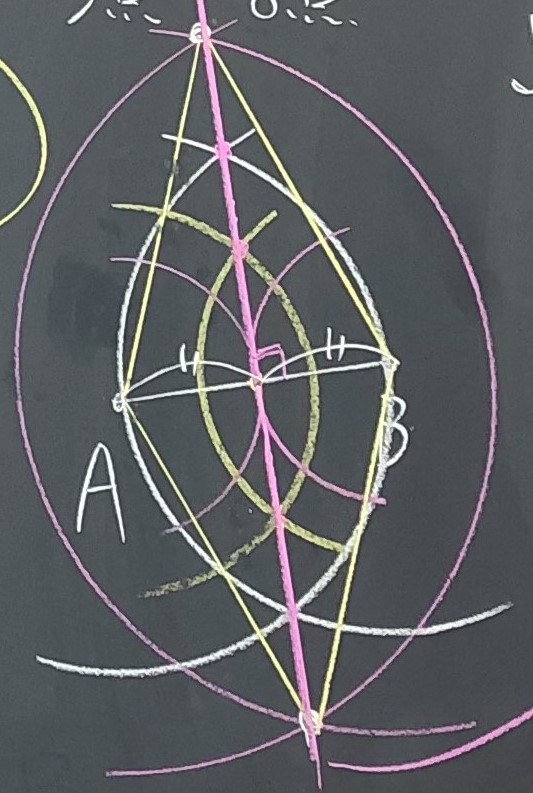
(複数の)ひし形ができ、点AとBは固定されているので、同一線上にできることを確認します。その後、点Aと点Bから等しい距離の点の集合が直線となることをまとめ、その直線はABを垂直に二等分することを確認しました(ひし形の対角線の性質)。