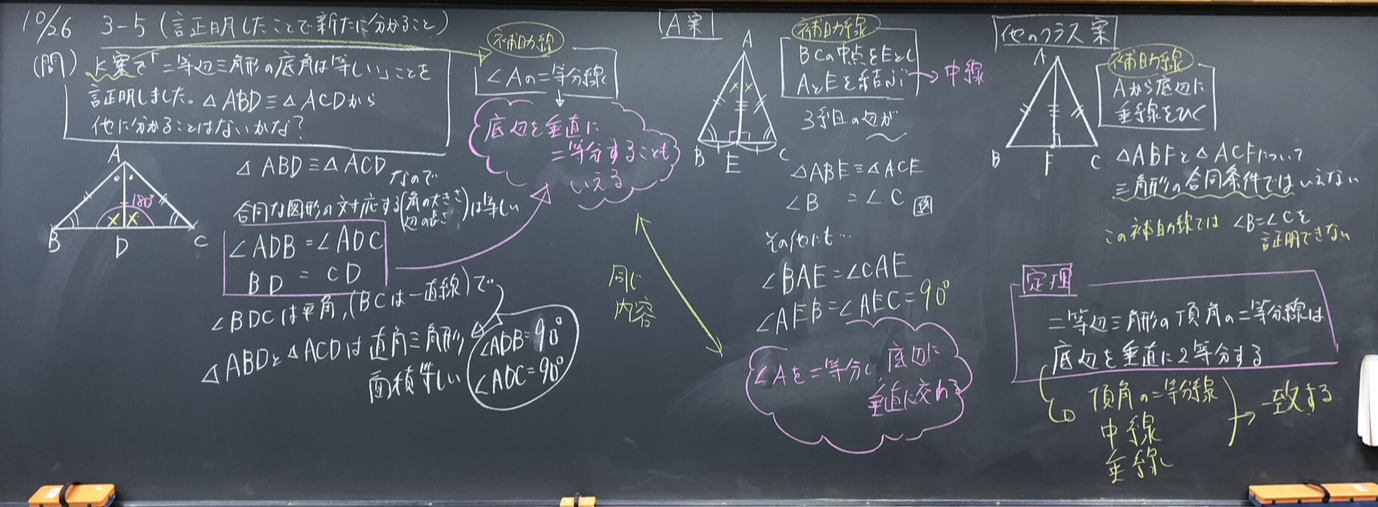
① 問題提示・解決(15分)
(問題)
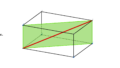
二等辺三角形の底角は等しいことを証明しました。この証明の内容から他に分かることを見つけましょう。
前時では、二等辺三角形ABCの頂角Aから二等分線を引き、底辺との交点をDとし、証明しました。
前時の内容を生徒に確認させてから、△ABD≡△ACDから他に分かることを考えてもらいました。

T「△ABD≡△ACDから他に分かることはありますか。周りの人と話し合ってみましょう。」
2分くらいしてから、全体で確認しました。
S1「∠ADB=∠ADCが言えると思います。」
T「それはなぜですか。」
S2「合同な三角形の対応する角の大きさは等しいからです。」
T「そうですね。他にありますか。」
S3「合同な三角形の対応する辺の長さは等しいので、BD=CDです。」
T「根拠まで言ってくれて、ありがとう。」
他にも△ABD=△ACDなども出ました。∠ADB=∠ADC、BD=CDから頂角の二等分線は底辺を垂直に二等分することをまとめました。
② 課題提示(5分)
(課題)
他の補助線でも、底角が等しいことを証明してみよう。
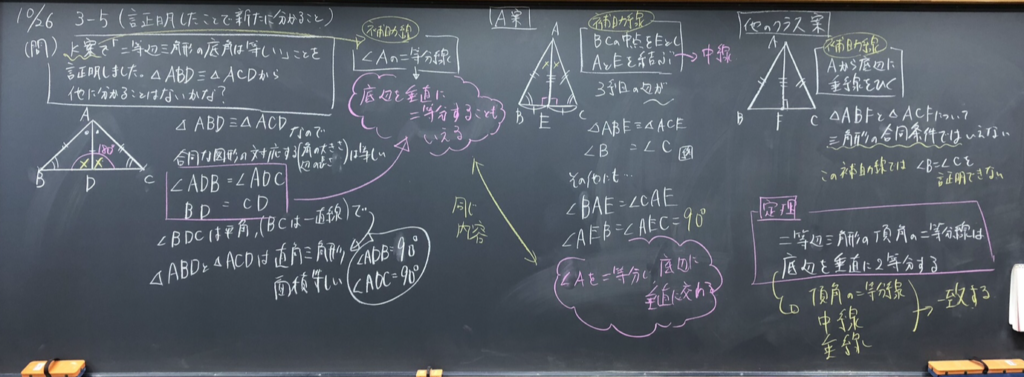
前時に二等辺三角形の底角が等しいことを証明するにあたり、補助線の案を出してもらいました。
前時の補助線を確認し、扱えなかった中線と垂線について考えました。
③ 課題解決(20分)
生徒には、中線と垂線のどちらから解いてもよいと伝えていますが、全体で確認する順は中線→垂線です。
中線
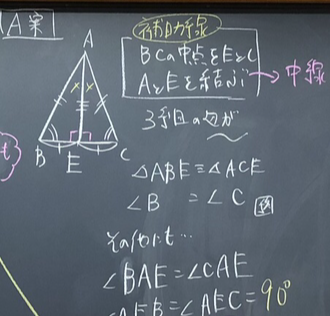
頂点Aから底辺BCの中線を引き、交点をEとします。頂角の二等分線と底辺BCとの交点はDとしました。最終的に点Dと点Eは同じ点になりますが、この時点ではあえて点Eとしました。振り返る活動でまとめるためです。
中線の補助線を使った証明では、
・定義より、AB=AC
・中線より、BE=CE
・共通な辺なので、AE=AE
3組の辺がそれぞれ等しいので、△ABE≡△ACE
合同な図形の対応する角の大きさは等しいので、∠B=∠C
T「この証明から他に言えることはないでしょうか。」
S1「合同な図形の対応する角の大きさは等しいので、∠BAE=∠CAE」
S2「合同な図形の対応する角の大きさは等しいので、∠AEB=∠AEC」
S3「∠BECは平角(180°)だから、∠AEB=∠AEC=90°です。」
S4「さっきのまとめた内容(頂角の二等分線は底辺を垂直に二等分すること)と同じですね!」
垂線
二等辺三角形の頂点Aから底辺BCに垂線を引き、交点をFとします。このとき、△ABFと△ACFについて合同であるか、考えていきます。
T「△ABFと△ACFは合同といえましたか。」
S1「2組の辺とその間の角がそれぞれ等しいので、合同といえるのではないでしょうか。」
S2「間の角は等しいかな。」
S3「定義からAB=ACで、垂線を引いたのだから、∠AFB=∠AFCです。また、AFは共通な辺です。」
S4「∠AFBと∠AFCは2組の辺の間ではないんじゃないかな。」
S1「そうか、間ではありませんでした。」
T「よく気づきましたね。それでは、三角形の合同条件は満たせていませんね。」

この補助線では、∠B=∠Cを証明できないことを伝えると、不思議そうな顔をしている生徒もいました。ただし、今後この考え方から新たな合同条件(直角三角形の合同条件)が言えることを伝えました。混乱しそうな生徒もいたので、直角三角形の合同条件の詳しい話は今後にとっておきました。
④ 振り返る活動(5分)
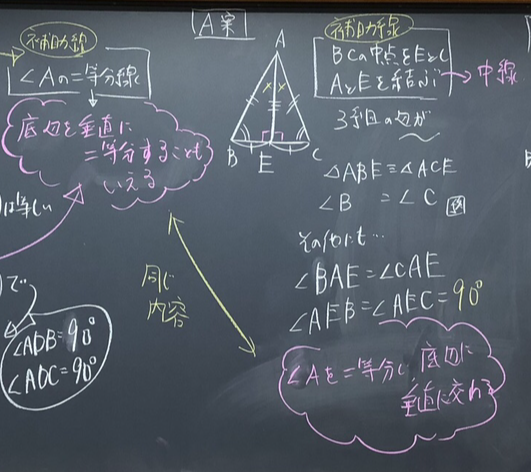
振り返る活動では、前回証明した内容から、「二等辺三角形の頂角の二等分線は底辺を垂直に二等分すること」も言えたことを伝え、定理としました。
また、これまで証明に用いた補助線
・頂角の二等分線
・中線
・垂線
これらは一致することを理解し、底辺との交点D、E、Fも同一の点であることを納得して本時を終えました。