コード系の物をカバンの中に入れて、数時間後に出してみると
どうやったらこんな絡まり方できるの!?とつっこみたくなる数学教師
#知らない間に誰かが絡めた説
#解くために2分はかかる
#自分で絡めたんだから自分で直ってほしい
1⃣ 問題
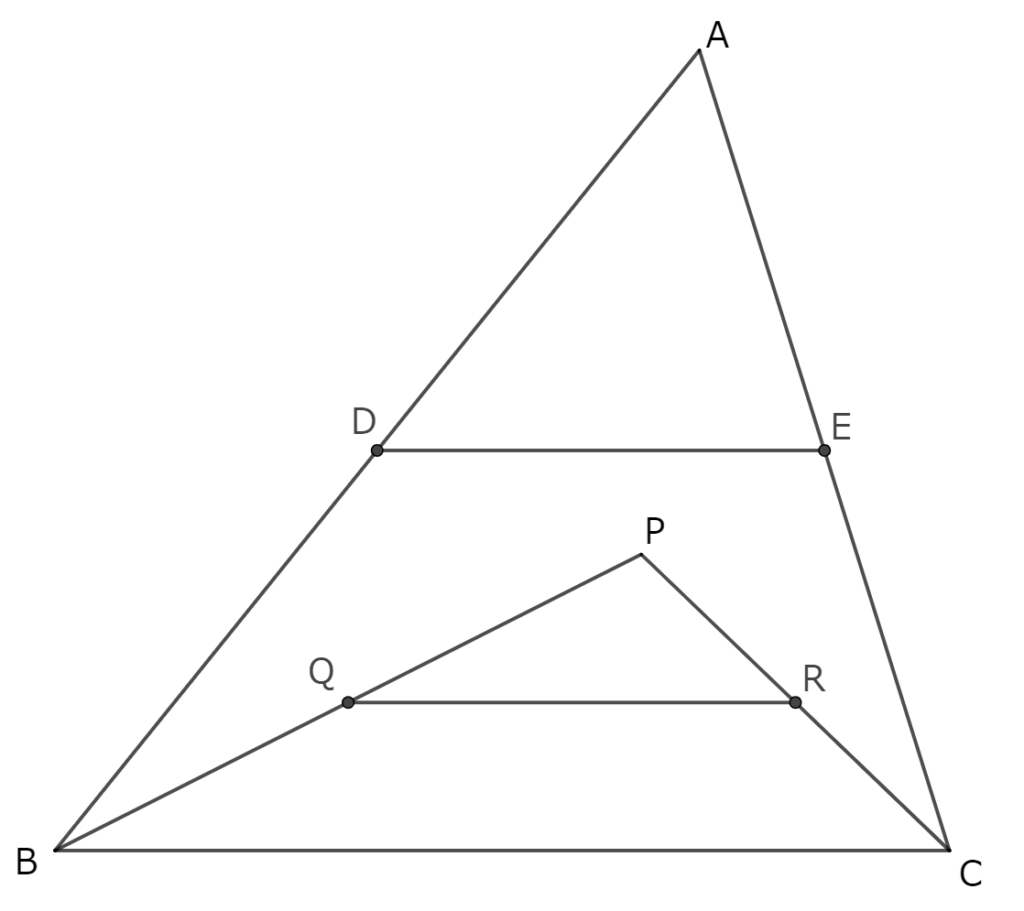
△ABCについて,ABとACの中点DとEを結びます。また,△PBCについて,PBとPCの中点QとRを結びます。このとき,DEとQRはどちらが長いでしょうか。
2⃣ 活動の流れ
本時は、上記の問題解決を通して、中点連結定理につながる証明を説明することを目標にしている。問題の図を初めから、教師側から提示してもよいし、問題文から生徒に図をかいてもらう流れでもよい。生徒がかく図形は、定規などを用い、なるべく正確にかかせたい。もちろん教員も。
問題に対する予想を生徒にしてもらうことが大事である。予想することで、主体的に取り組む態度が望めるためである。予想と現実のギャップがあればあるほど、生徒の記憶に残ると考える。
問題解決は各自思考(約5分くらい)おこなう。しっかりと証明をかかせることも大事だが、本時ではその後も適応問題の時間を設けたいため、説明程度のメモでOKとした。教師は各自思考の中でできない生徒へのフォローをおこなう。
各自思考後はグループや近くの人と確認の時間を設ける(3分くらい)。その後、全体の理解度も見ながら、DEとQR長さについて説明する。時間経過をみて、教師主導でも生徒主導でもよい。本時では生徒が説明をした。

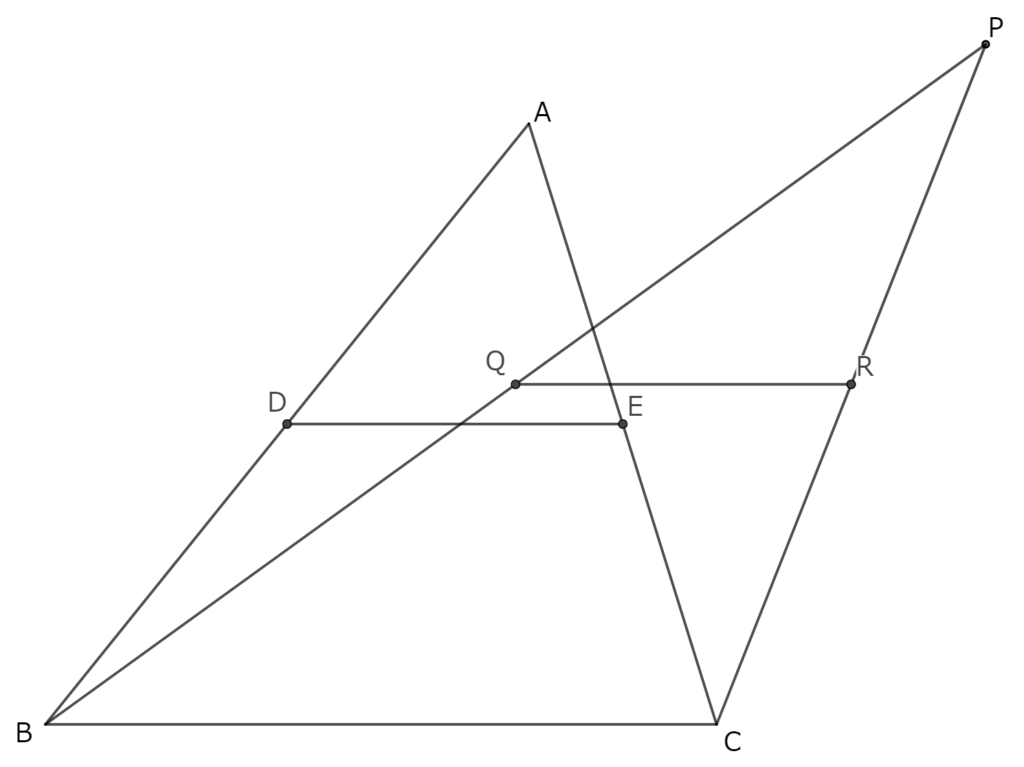
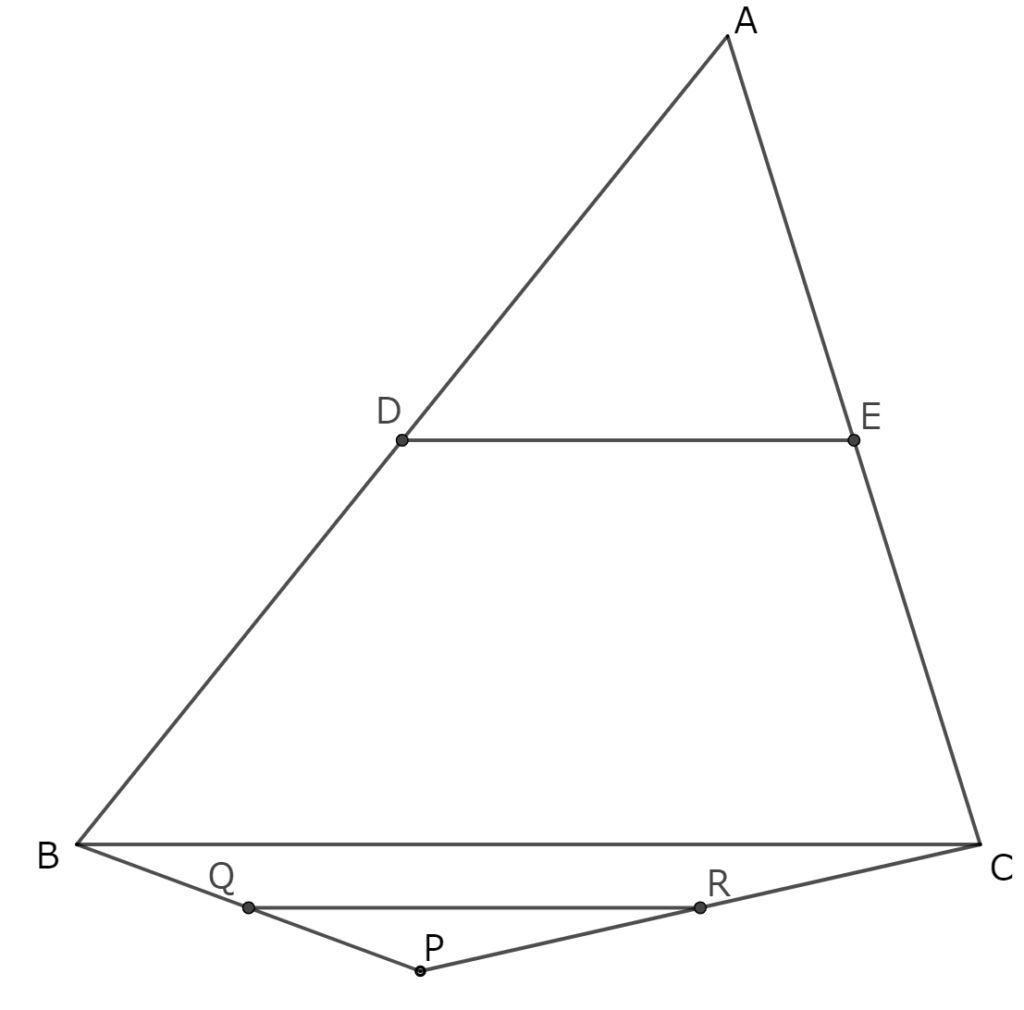
DEとQRの長さについての問題解決後に、点Pがどこにあっても(動こうとも)DE=QRの関係は変わらないことを、考えさせる時間をつくりたい。生徒に図をかいてもらう場合は、△ABCの外部に点Pがある場合の図を取り上げやすい(最初からどちらの図も提示してもよい)。
生徒から点Pが動くことを引き出すには、最初の問題ですぐに解決した生徒を生かしたい。普段から問題の条件変えの見方を養うことが大事になってくる。また、教師の仕掛けとしては、あえて点Pとしたところにもある。
DEとQRが平行であることにも気づかせたい。各自思考の中で、DとQ、EとRを結んでいる生徒を巡回の中で見つけておくとよい。その生徒がかいた補助線を提示して、四角形DQREがどのような形であるかを問う。平行四辺形であることの予想はつくと思うので、図2、3、4でも成り立つかも考えさせる。
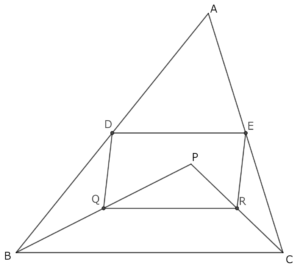
平行四辺形になるための条件を確認し、中点連結定理の内容をまとめる。その後、図6の適応問題に取り組む。
(適応問題)
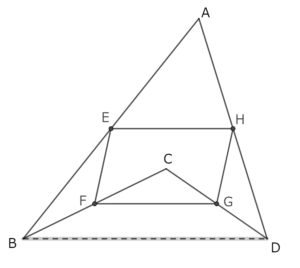
四角形ABCDの辺AB,BC,CD,DAの中点をそれぞれE,F,G,Hとするとき,四角形EFGHは平行四辺形であることを証明しよう。
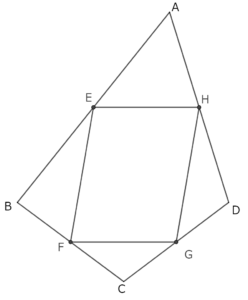
適応問題に対する証明は省略する。適応問題の解決後に、最初の問題を見比べ、統合的な見方を養いたい。点Cを移動すると、最初の問題と同じになる。下図参照。
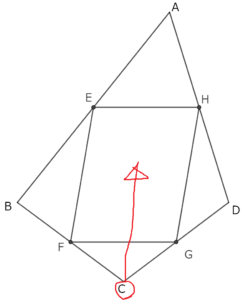
読んでくださった方の人生がいつまで輝き続けますように。