今まで食べられなかったものが、急に食べられるようになっている成長期な数学教師
#ミョウガとシナモンいけたよ
#早くパクチーいきたい
① 問題1提示(5分)
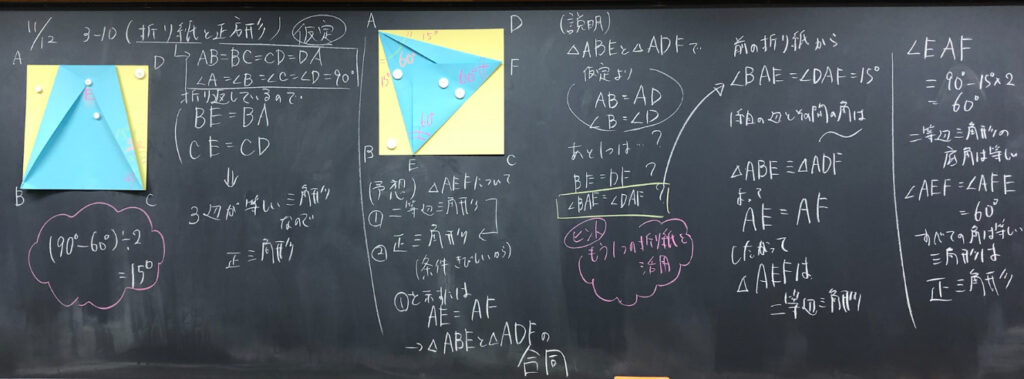
生徒一人ひとりに折り紙を配布します。折り紙は両面色付きだと考えやすいかもしれません。今回は予算的に、裏面は白色の折り紙を配布しました。
折り紙は正方形であることを確認してから、折り方を指定し、図1のようにしました。

「折り紙を使って、正三角形をつくろう」と問題提示しても、面白い授業になると思います。その場合は、授業の目標やねらいが変わってくると思います。今回は、折り方を指定することで、正三角形であることにも気付いてほしくて、このような流れにしました。
机間指導で、全員が指定した図形ができているかを確認し、問題を提示します。
(問題)
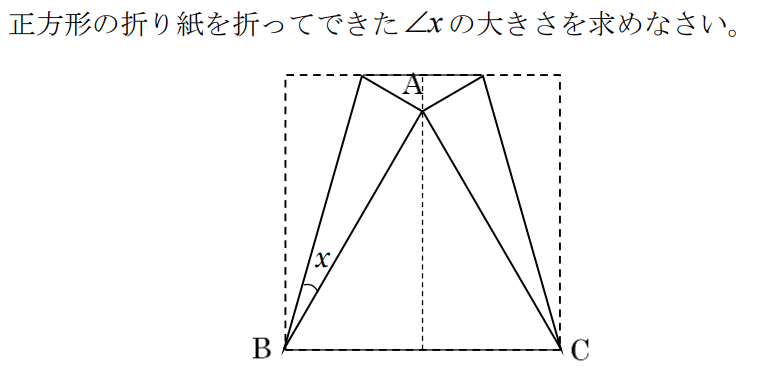
正方形の折り紙を折ってできた∠xの大きさを求めよう。
② 問題1解決(10分)
各自で思考したり、周りの生徒同士で思考したりと自由に考えさせました。感覚的に解ける生徒もいると思いますが、正方形の内部にできた三角形が正三角形になることの根拠をしっかりと抑えたいと考えています。

S1「△EBCが正三角形なので、∠x=(90°-60°)÷2=15°と求められました。」
T「S1さんが△EBCが正三角形であると話してくれましたが、どうしてそうなったのか、詳しく説明してくれる人はいますか。」
S2「正方形なのでAB=BC=CDで、折り返しているからAB=EB,CD=CEとなります。よって、EB=BC=CEとなり、三辺が等しいので、正三角形です。」
T「∠x=(90°-60°)÷2=15°の式の÷2の部分はみなさん理解していますか」
折り紙を折ることで、どこの辺や角度が同じになるのかをしっかりと抑えるために、発問しました。また、この後の問題に関係してくるからです。必要に応じて、(理解していなさそうな生徒が3割くらいいたら)近くの生徒同士で話し合ってもよいと思います(30秒~1分くらい)。
③ 問題2提示(7分)
問題1の解決後、再度、折り紙を配ります。折り方を指定しますが、問題1の折り方と似ているので、生徒が間違わないように、板書用に作った模造紙で説明します。また、机間指導で、全員ができているか確認も必要です。
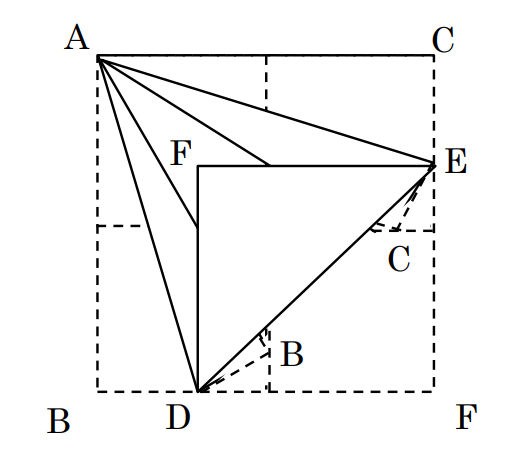
T「このようにできた三角形はどのようになってと思いますか。まだ、根拠はなくてよいので予想しましょう。」
先ほどの問題で根拠にこだわったので、少し考え込む生徒もいるかもしれません。この段階では、予想でよいことを強調しましょう。生徒の反応としては、二等辺三角形か正三角形の2つが挙がると思います。
③ 課題提示(7分)
(課題)
自分が予想した図形となることを、根拠をもって説明しよう。
今回の授業では、1時間で納めようとして、少し教師が誘導するような形になってしまいました。本当は、この課題解決だけで1時間を設けた方が、ゆっくりじっくり思考できよいと思います。
2つの予想となる、二等辺三角形と正三角形が出た時点で、どちらの説明の方が簡単かを問いました。正三角形を説明する方が条件が多いため、二等辺三角形の方が簡単であることを確認しました。
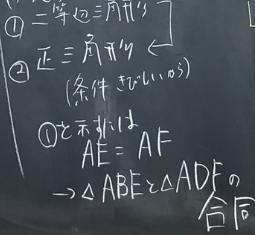
二等辺三角形であることを示すための筋道としてAE=AFが板書しました。生徒から同じ折り方をしているため、辺が等しいことの方が示しやすそうとのことでした。残り時間の関係で、辺に絞りましたが、本当は角度がひとしいこと(∠AEE=∠AEF)の発想も挙げた方がよかったと思います。
△ABEと△ADFが合同を言えればよいことまでを全体共有してから、課題解決の時間を設けました。
④ 課題解決(15分)
難しい課題のため、思考の時間は周りの生徒同士で話し合ってもよいし、各自で考えてもよいとしました。
5分後には、仮定を確認し(AB=AD,∠B=∠D)、三角形の合同条件を満たすために、あと何を示せばよいかを全体で共有しました。
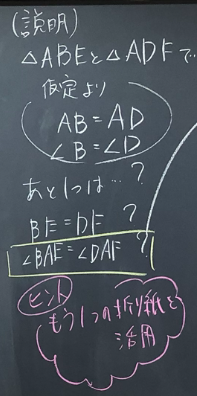
全体で共有した後、机間指導で二等辺三角形であることの説明ができた生徒を見つけます。その生徒には、残り時間で正三角形であることの説明もしてみようと声をかけました。
問題1の内容と関連付けて解けた生徒にヒントを出してもらいながら、全体で解決しました。
⑤ 振り返り活動(5分)
振り返る活動では、正三角形であることを説明する時間にしました。
T「二等辺三角形であることは説明できましたが、正三角形であることは説明できそうですか。」
今回は残り時間もなかったので、早くできた生徒に説明してもらいました。二等辺三角形の頂角が60°になることで正三角形となること説明となるため、生徒にとっては気づくのが難しかったように感じました。

EFが他の2辺と等しくなることで説明できるのではないかと考えている生徒もいたようです。1時間で収めようとせず、2時間の授業で思考する時間をたっぷりと取った方が良かったと感じました。

