① 問題提示(10分)
(問題)
箸を弁当の中にしまうことはできるだろうか。
紙で実寸の弁当と箸を作り、生徒に発問しました。
T「私の弁当箱に箸はしまえそうですか。」
S1「見た目では分からないです。」
T「この問題を解くにあたり、何か質問はありますか。」
S2「お弁当と箸の大きさは分かっていますか。」
T「はい。弁当の縦は12cm、横は16cm、箸は21cmあります。」
T「他に質問はありますか。」
S3「弁当箱の形は、長方形ですか?」
T「はい。長方形とします。他にはありませんか。」
解けそうな表情をする生徒が多くなったところで、各自思考の時間をとりました。
② 問題解決(10分)
クラスの全員が長方形の対角線を求められることを目標に、机間指導に臨みました。
(机間指導でおこないたいこと)理解度順
△:問題解決のために、何を求めればよいか分からない。
→箸が長方形の縦や横の長さより長いため、入らない。
しかし、長方形ではどこの長さが一番長いかを問い、対角線の長さを求めるように導く。
三平方の定理に感づかない生徒には、長方形の直角に注目させる。
◇:長方形の対角線の長さを求めることができる。
○:解を求めることができる。その解が適しているのか、確認している。
また、現実の世界と照らし合わせて、箸が入る方法を考えようとしている。
7分くらい経ったところで、B評価の生徒に板書してもらいました。机間指導の中で、予めお願いしました。
三平方の定理を用いて、長方形の対角線の長さは20㎝と求められます。箸の長さが21㎝なので、長方形の対角線にはしまえない(収まらない)ことになります。
③ 課題提示・解決(20分)
T「長方形の対角線には箸はしまえません。どうしたらよいでしょうか。」
S4「お弁当は平面じゃなくて立体(高さがある)から、斜めにして入れられないでしょうか。」
T「いい考えですね。S4さんの話してくれたこと伝わったでしょうか。」
直方体の対角線の考えが生徒から引き出せない場合は、実際のお弁当について、具体的に考えてもらいます。
(課題)
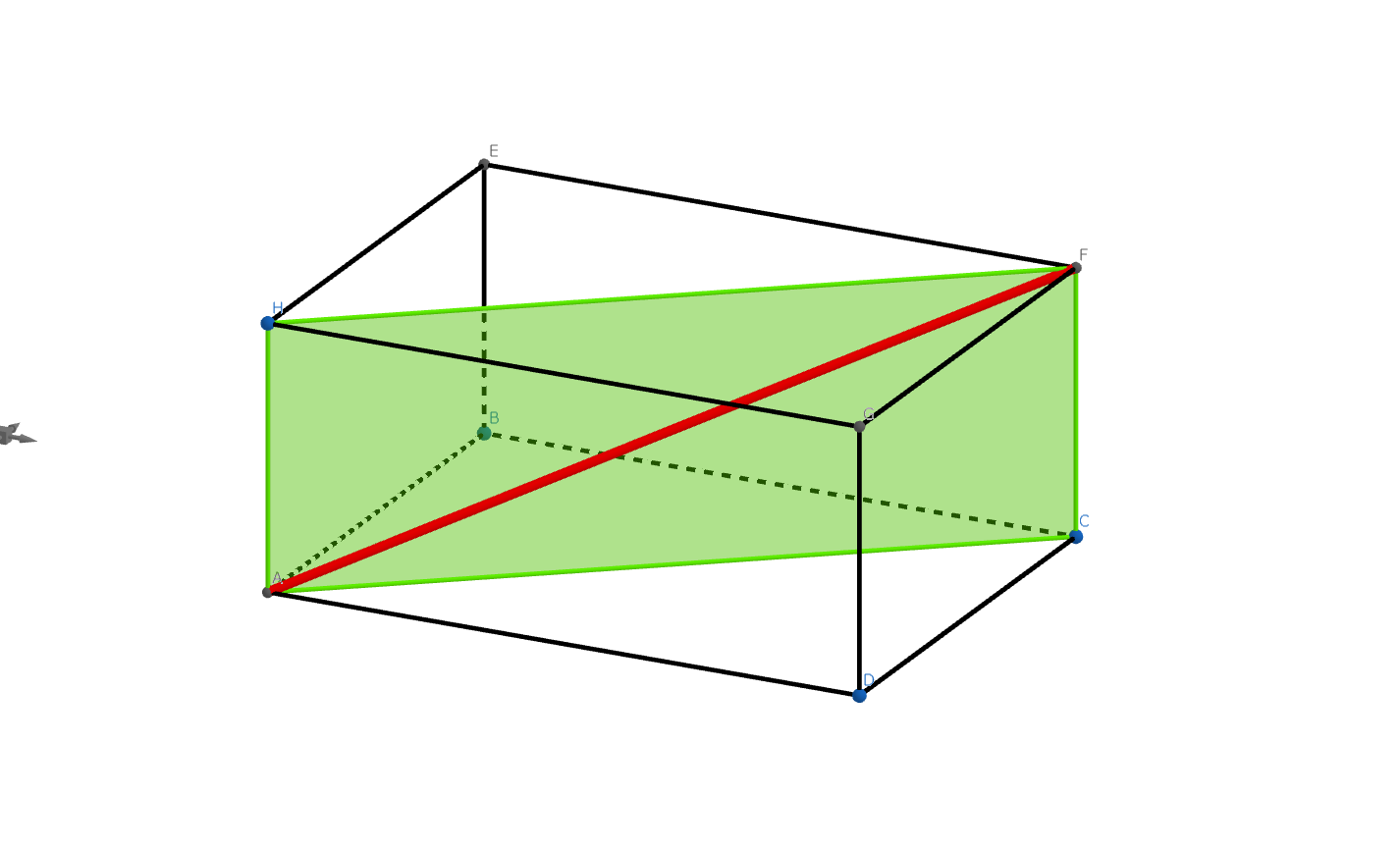
お弁当の高さは7㎝の直方体とします。箸はしまえるでしょうか。
直方体の対角線について、求める部分を確認します。
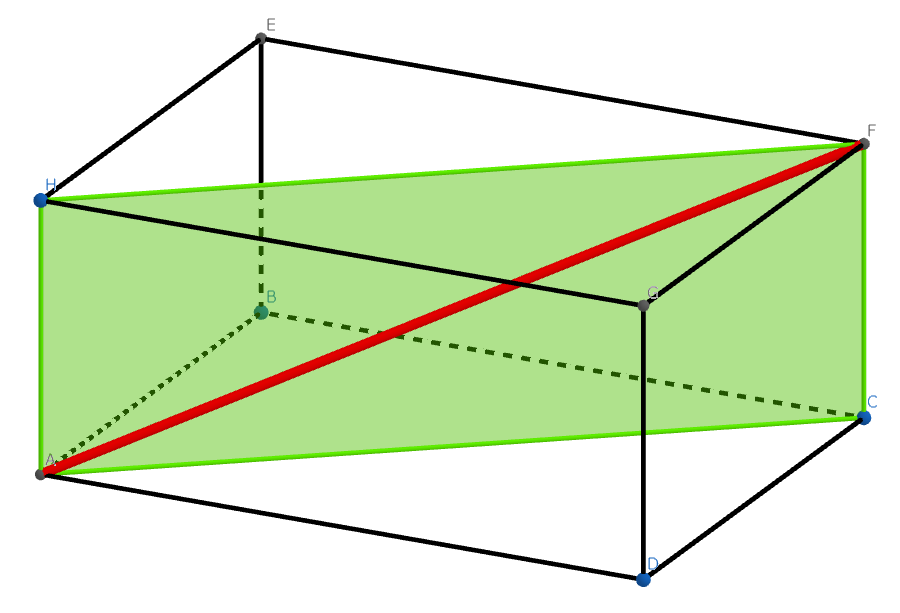
すらすらと三平方の定理を使って解き始める生徒も多くいると思います。3分くらい経ったところで、三平方の定理を用いた式のみ板書してもらいます。
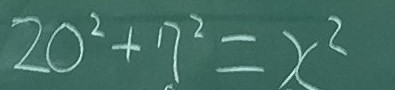
T「○○さんに式を書いてもらいましたが、なぜこのような式を立てられたのでしょうか?」
S5「切断面の直角三角形から、三平方の定理を用いて、式を立てたのだと思います。」
T「なるほど、切断面から直角三角形がつくれるのは、みなさん分かりますか。」
生徒同士が話し合う時間をつくります。
・なぜ直角になるか分からない生徒
・あいまいな理解で説明する生徒
・根拠をもって説明する生徒 など
様々な生徒がいると思います。机間指導しながら、どのような反応にも受け止めます。特に分からないときちんと言える生徒を肯定するように心掛けます。そのような生徒を肯定することで、あいまいな理解であったことを認知する生徒も出てきます。生徒同士の話し合いの中で、理解を深めていく時間にしたいと思っています。
直方体の切断面が長方形になっていることの確認は、実際に具体物(消しゴムや発泡スチロールなど)を見せてもよいし、ジオラマでもよいと思います。また、上と下の面が平行の位置関係から、直角になることを納得させることも大事です。
三平方の定理を用いて、直方体の対角線の長さを求められたら、次は解の吟味です。
解の√449と箸の21の大小関係を確認し、箸がしまえる結論になりました。
S6「先生、箸の太さは考えなくてよいのでしょうか。」
T「S6さん、現実的に考えている発言で素晴らしいですね。実際には太さも関係してくると思います。」
S7「でも、蓋が柔らかかったら、なんとかしまえるかもよ!」
現実的に考えられるようになってきた発言も肯定しながら、キリが良いところで振り返る活動の時間を設けます。
④ 振り返る活動
深さが6㎝ならしまえたのだろうか。
結果の予想を聞いても良かったと思います。1㎝変わると21㎝の箸にどのように影響してくるのか、感覚的に聞くことで、より主体的に解き始めるかもしれません。
△:解けない→先ほどの問題と比較して、解くように促す。全員が◇になるように、教師は努める。
◇:解と求めることができる。
○:解を求め、吟味もおこなうことができる。
◎:箸がしまえる深さの最小値を求める、直方体の対角線について一般化した式を導くなど。振り返る活動で与えられた問題以外で、自ら問題を作り解くことをしている。
まとめの時間では、直方体の対角線について、一般化した式を書き本時を終えました。