どちらがチップでどちらがデールなのか、いまだに分からない数学教師
#よく見たら全然違う
#この2人は兄弟?ただの仲良し?
① 問題提示(5分)
初めに定義について説明し、二等辺三角形の定義を話しました。そして、小学校で習った性質を全体で共通しました。小学校で習った二等辺三角形の性質は、具体的な事象を使って確かめだけだったので、「文字を使って証明しよう」と問題提示しました。
(問題)
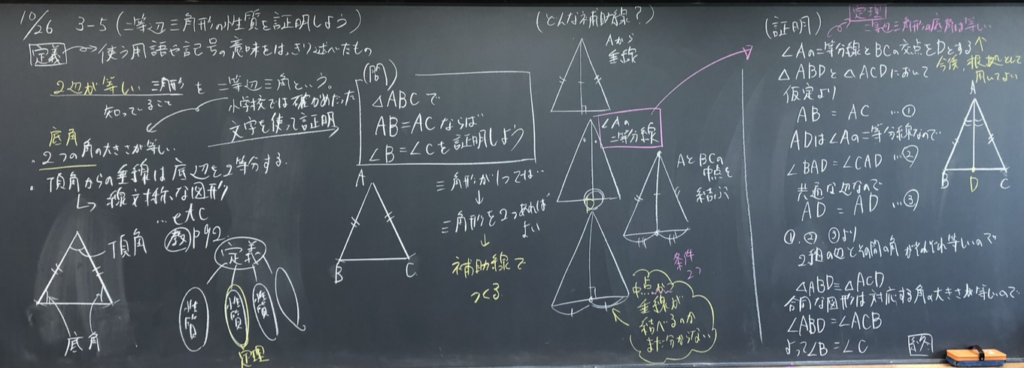
△ABCでAB=ACならば、∠B=∠Cであることを証明しよう。
図を書いて、証明の道筋を全体で確認しました。
T「この証明をするにあたり、どんなことが困っていますか。」
S1「これまで証明問題は三角形が2つ(以上)あったけど、今回は三角形が1つしかありません・・・。」
T「どうすればよいでしょうか。」
S2「三角形が2つあれば・・・」
S3「補助線を引けば、いいんじゃないかな?」
T「なるほど、では補助線を引いて、三角形を2つつくってみましょう。」
② 課題提示(5分)
(課題)
問題をつくための補助線を考えよう。
生徒の予想される反応としては
・頂角の二等分線をひく
・頂角から中線をひく
・頂角から垂線をひく
を考えていました。
机間指導の中で、「頂点から垂直二等分線をひく」という考えがあったので、おもしろいと思い、全体で共通しました。
③ 課題解決(10分)
全体で補助線の内容を共有しました。時間の関係で、生徒の発言ではなく、私の方で4種類の考えを板書しました。

T「先生が見て回って、4種類の補助線の案がありました。他の補助線をかいた人いますか。」
S「・・・(いない)」
T「いい考えがたくさん出ました。これらの補助線の案で証明は進めていけそうですか。」
生徒の表情などから、4種類全部できそうな雰囲気があったので、「頂点から垂直二等分線をひく」内容に注目させるような発問をしました。
T「実はこの中で、この補助線では、証明を進められない内容があります。どれか分かりますか。」
S4「頂点から垂直二等分線って、(小学校で習ったから)分かってるけど、使っていいのかな。」
中学では小学校で習ったことを文字を使って証明していくことを始めに話しました。そのことが頭に残っていて、このような発言になったのかもしれません。
他のクラスで授業したときには、「頂点から垂直二等分線をひく」考えだけ、「シンプルじゃない」とか「条件が多い」などの発言から、仲間外れ感で選んでいました。
T「頂点からの垂線が底辺を二等分するかどうかが、分かりません。よって、4つ挙げてもらった補助線のうち、3つから説明しています。今日は「頂角の二等分線をひく」補助線に絞って考えていきます。他の補助線は次回の時間で確認していきましょう。」
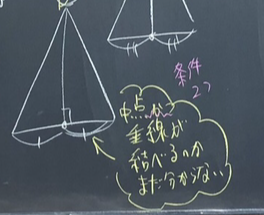
「頂点から二等分線をひく」補助線に絞ったのは、循環論法にならないように配慮しました。ユークリッドの補助線を紹介した年度もありました。
④ 問題解決(10分)
まだ、証明問題に慣れていないこともあり、十分に時間を確保しました。なるべく、全員が解決できるように机間指導で助言します。また、早くできた生徒は、他の補助線で解決する姿もありました。解決方法を絞ること(他の補助線でやりたかった生徒の気持ちをくすぐること)で、そのような姿が望めます。

⑤ 振り返り活動(5分)
振り返る活動では、今回証明した内容が今後「定理」として根拠として活用できることを話して終わりました。